第二節　スキーマとストラテジーの幾何学的モデル

3-2-1 スキーマとストラテジーの幾何学的表示

　　　　　　　　　　　　　　　　　　　　　　　　　　　　●初期状態

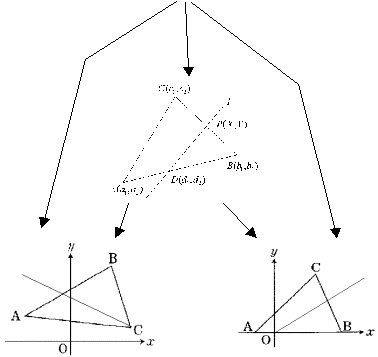
第一節で述べてきた経過を

幾何学的に表現すると右のようになる。

　先ほどまで挙げていた問題が一連の　　　　　　　　　　�B

スキーマを構成していることがわかる。

　このひとつひとつの問題を繋げて

いるものは何であろうか。

「初期状態→�@」としているものは、

「高さを共有している」性質を

利用し、「面積比から底辺比」へ

「次元を落とす」という考えで

ある。

　　　　　　　　　　　　　　　　　�@　　　　　　　　　　　　　　　　　�A

　　「初期状態→�B→�@」「初期状態→�B→�A」は「一般性は高い」が手間がかかる。しかし、

演算を自動化させればほぼ確実に結果を導くことができる。

　「初期状態→�A」は、通る点が原点であったという特殊性によって解決が易しくなっている

ことがわかる。

この図全体がスキーマともいえるし、その問題場面に対して問題解決者が知っている範囲が

知識スキーマである。知らない部分は、解決の際に発見的にならざるを得ない。

　また、このスキーマそのものを知識としてもち、同じ問題であれば、そのスキーマをアルゴ

リズム的に用いて、ルーチンな解決を図る。これが、「四角形を二等分する」ような問題に対して、

「類推的に働く」こともある。このとき、初めて解く問題であれば、ノンルーチンで「類推の考え方」

をストラテジーとして用いた、と考えられる。

　つまり、「数学的な考え方」は、後から見れば、「ルーチン」でも「ノンルーチン」でもかまわない。

しかし、ルーチンな解決をしたとき「数学的な考え方」をストラテジーとは呼びにくい。それが発見的

な解決ではないからである。

3-2-2 考察

　いま述べてきたものをまとめて、ストラテジーとスキーマの関係を幾何学的モデルにすると、

次の３通りが考えられる。

�@ すでにあるスキーマから選択するストラテジー

　�A スキーマを拡張するストラテジー

　�B 新しい問題場面でスキーマを作ろうとするストラテジー

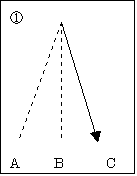�@ ある問題に対して、用いるべき手段・知識が揃っているが、

「どの手段を用いればいいか見出せないでいる」とき、我々は数を

代入したり（具体化・特殊化）といった手段で、解決の計画を立てる

はずである。実際に選択されたストラテジーは、既知のもので、「解法」

と呼ばれたり、「数学的な考え方」と呼ばれたりする。

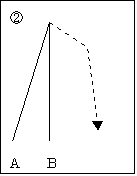�A A,Bの形式の問題は、解いたことがあるが、直面している問題は

まだ解いたことがない。そんなとき我々は、あらゆる「数学的な考え方」

を用いて解決を試みる。このとき「数学的な考え方」はストラテジーと

して用いられたと考えられる。

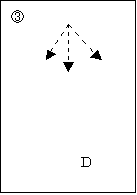
�B 全く知らないと思われる問題場面に直面したとき、我々は既存のスキーマ

やストラテジーを使って解決できないかと検討するはずである。この検討に用

いた「数学的な考え方」は、ストラテジーとして機能しているはずである。

　つまり、問題場面を次の３つに分けることができる。

�@ ほとんどルーチンな問題場面

�A ルーチンな部分もあるが、ノンルーチンな部分もある問題場面

�B ほとんどノンルーチンな問題場面

�@ にある「ほとんど」というのは、「わずかなノンルーチン部分」つまり、ストラテジーを選択したり、

解法を当てはめるための工夫をしたりといった余地を残した問題のことである。

　すでに知っている問題の類似問題を解く際に、まったく工夫せずに既有知識を転移（当てはめて解く）

できることはほとんどない。だからこそ、「例題を覚えたが、練習問題を解くことができない」ということが

起こるのである。

�A にある「ほとんど」というのは、「全く既知の部分のない問題」では、問題の中に切り崩す余地がなく

なってしまうからである。一見、全くしらない問題であっても、その中には必ず既有の知識を必要とし、

その部分を発見することによって解決を図ることになる